A maths wizard has discovered the largest known prime number and it’s an amazing 17 million digits long.
Curtis Cooper, of the University of Central Missouri, in the US found it by using hundreds of computers networked together.
You might not have to be a maths genius to know that a prime is a number greater than 1, which can only be divided by itself and 1, like 2, 3, 5, 7, 11, but to find one that big, GCSE maths would be a good start.
However, in the numbers world, size doesn’t matter when it comes to fascination and strangeness.
1. Hailstone Numbers
There are many simple questions about numbers that no one has been able to answer.
Start with any number—if it is even, divide it by 2; if odd, multiply by 3 and add 1. Then keep going, writing down the sequence of numbers that you generate. For example, starting with 7 we are led by these rules through the sequence:
7 -> 22 -> 11 -> 34 -> 17 -> 52 -> 26 -> 13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1.
It seems no matter what number you start with. You eventually hit a 1. These sequences are called the “hailstone numbers” because, like hailstones, they go up and down a number of times before inevitably falling to Earth. However, no one has been able to prove that this has to happen every time.
2. Twos, Threes & Fives
Think of a number. Add 4, then multiply the result by 4. Subtract 8, then divide the result by 4. Finally take away your original secret number. The answer is 2.
Think of another number.
Double it. Add 9. Subtract 3. Divide by 2. Subtract your original number. The answer is 3.
Think of any three-digit number.
Add 7. Multiply by 2.
Subtract 4 and then divide the result by 2.
Subtract it from the original number you thought of.
The answer is 5.
3. Ninety-Nine
Write down any two different numbers from 1 to 9. Then reverse the two numbers.
You should have two two-digit numbers.
Subtract the smaller number from the larger one.
Take the result, reverse the digits and add that number to the one you got when you subtracted.
The answer is 99.
For example: 72 reverses to make 27.
Subtract the smaller (27) from the larger (72): 45.
Reverse these digits to make 54.
Add this to the previous number.
The answer is 99.
4. Three Does It
You can discover whether a number is a multiple of 3 just by checking whether this is true for the sum of its digits.
For example, 12,894 has 1 + 2 + 8 + 9 + 4 = 24 = 3 x 8, so 12,894 is a multiple of 3.
You don’t need to do the long division in order to find this out.
You can do this even for huge numbers that your calculator could never cope with.
For example, try: 111,222,333,444,555,666,777, 888,987. Is it divisible by 3? In fact, if you’re clever, you might be able to give the answer before summing the digits.
5. 10% Up Then 10% Down Means You Lose Out
A worker’s boss explains that in order to stay competitive he will have to cut his pay by 10% but he will allow the employee to work 10% more hours to make up for it, “so your pay will be maintained”.
Afraid not! If the worker was being paid, say, £100, the 10% cut takes him down to £90. The 10% extra hours will add back on 10% of £90, which gives him £99. He is still £1 worse off. Beware percentages—you need to know what they refer to.
6. Never-Ending Squares
Square numbers (the products of numbers multiplied by themselves) and prime numbers are important and your Internet security only works because the prime numbers never run out.
You can get the endless list of squares just by adding the odd numbers up: 1 = 1 x 1, 1 + 3 = 4 = 2 x 2, 1 + 3 + 5 = 9 = 3 x 3, 1 + 3 + 5 + 7 = 16 = 4 x 4 … and this pattern never lets you down.
However, when it comes to primes, we still have to go out hunting for them, which is why at any one time there is always a world champion largest known prime.
7. ‘Mind Reading’ Trick
Choose a single-digit number, multiply it by 9 and if the answer has two digits add them together.
Subtract 5 from what you have, giving you a number. Turn the number into a letter by the rule A = 1, B = 2 and so on. Think of a country beginning with your letter. Take the last letter of your country and think of an animal that begins with that letter. It’s odds on that you have a kangaroo in Denmark.
8. It All Adds Up… To 9
1×9=09 =0+9=9
2×9=18 =1+8=9
3×9=27 =2+7=9
4×9=36 =3+6=9
5×9=45 =4+5=9
6×9=54 =5+4=9
7×9=63 =6+3=9
8×9=72 =7+2=9
10 x 9 = 90 = 9 + 0 = 9
9. A Truly Remarkable Number
Enter 999999 into your calculator and then divide it by seven.
The result will be a mysterious number!
Throw a die (or randomly pick a number from 1 to 6) and multiply the result by the mysterious number.
Arrange the digits of the product from lowest to highest from left to right to form a six-digit number.
What is the number?
Answer: 124578
10. Number Names
Think of any number from 1 through 100. Write down its name.
Count the number of letters in its name to obtain a second number. Count the number of letters in the second number to obtain a third number.
Continue in this way until the chain of numbers ends on a number that keeps repeating.
What is the number?
Answer: Four
11. The Magic of 8
Multiply your phone number—treating it as a seven-digit number (without its area code)—by 8. Then write down the following three numbers:
(i) your phone number,
(ii) 8, and
(iii) the product of your phone number and 8.
Add up all the individual digits in those three numbers. If the sum is more than one digit, take that sum and add up its digits. Continue adding up digits until only one digit is left.
What is the digit?
Answer: 8
12. Secret Word
When in the course of human events, it becomes necessary for one nation to dissolve the political bands which have connected them with another, and to assume, among the Powers of the Earth, the separate and equal Station to which the Laws of Nature and of Nature’s God entitle them, a descent Respect to the Opinions of Mankind requires that they should declare the causes which impel them to the Separation.
Printed above is the first paragraph of the U.S. Declaration of Independence. Select any one of the first 20 words. Count the letters and call that number n. Move ahead n words, beginning with the word after your selected word. When you reach that nth word, count its letters and move ahead as many words as the new letter-count. Continue in this manner, counting letters and moving ahead words, until you stop on a word that’s beyond the fourth line.
On what word did you stop?
Answer: God
13. A Number Trick…
1. Think of a number from 1 to 10
2. Multiply it by 9
3. Add the digits together
4. Subtract 5
5. Find the letter of the alphabet which corresponds to your number (1 = A, 2 = B, …)
6. Think of a country that starts with that letter
7. Think of an animal that starts with the last letter of your country
8. Think of a colour that starts with the last letter of your animal
9. What do you mean?
Answer: Orange Kangaroo in Denmark
14. Phone Number Trick
1. Get a calculator. (You won’t be able to do this one in your head)
2. Key in the first three digits of your phone number. (NOT the area code)
3. Multiply by 80.
4. Add 1.
5. Multiply by 250.
6. Add the last 4 digits of your phone number.
7. Add the last 4 digits of your phone number again.
8. Subtract 250.
9. Divide the number by 2.
Do you recognize the answer?
15. At What Age Should You Get Married?
I like this one. It uses Euler’s number (e, which roughly equals 2.71828) to tell you the age where you have the highest probability of getting married to the ideal person.
1. Figure out the age range when you consider yourself marriageable. If you’re already well into it, let’s say 22 to 45. (If you’re in rural area, go ahead and switch that down to 18 to 24. If you’re in a major city, feel free to pump it up to 31 to 86.)
2. Subtract the oldest age from the youngest age to calculate your total number of the years of marriage.
3. Divide that number by e, or 2.71828.
4. Add the result to your youngest marrying age.
So if you’ve set a range of 22 to 45, that’s 23 years. Divided by Eular’s number is 8.46. Added to 22 is 30.46, meaning that between 30 and 31 is the time when you’re at your statistical peak (and ready to stop messing around with data points and settle down with that one special data point).
16. Power Multiplication Or Square Of A Number That Ends In 5
Here the speed would really amaze you. Try finding the square of 85 in your head. How much time did it take you? Now try this fast mathematical trick here.
1. Ignore 5 in the units place
2. Take the digit in the tens place, i.e. 8 and multiply it with its successor, i.e. 8+1 = 9. The result is 72
3. Simply place 25 at the end of the result, i.e. 7225. That’s it. 7225 is the square of 85. That is your answer.
Wasn’t that a fast mathematical trick? This mathematical trick can be used anytime you have to find square of a number ending in 5. It works with 3-digit numbers too. So the square of 135 is ….. first multiply 13 by its successor, i.e. 14 = 182. Now add 25 at the end. Your answer is 18225.
17. Be A Maths Wizard (Or Mind Reader)
Here is a mathematical trick you can play on your friends to show them what a maths whiz you are! Tell a friend that the two of you will pick five 5-digit numbers at random, and then will add them together—but, amazingly, after just hearing the first number and before the others have even been selected, you’ll be able to predict accurately what the TOTAL of those five numbers will be!
Steps:
1. Have a friend write down a 5-digit number—for example; he might write down 67,812.
2. Then on a separate piece of paper, you can immediately write down the final “answer” to this quiz (the total of all five numbers), even though four of the numbers haven’t even been selected yet! For the example given, 67,812, the answer will be 267,810.
3. Announce that you have “predicted” the final answer and written it down as proof—but don’t show it yet. Just fold the piece of paper over to keep that answer hidden till the end of the “trick”.
4. Then have your friend write down a second 5-digit number right beneath the first one.
5. You then quickly write down a third 5-digit number right below it (but you’ll have to know what to write—to find out, visit the instructions below!).
6. Then have your friend write a fourth 5-digit number under your number. Then you immediately write a fifth 5-digit number beneath it (again, you’d select that number according to the instructions below).
7. Then ask your friend to add up the five 5-digit numbers that have been written down.
8. Compare that answer to the one you wrote down after the first number was selected.
Amazingly, they will be identical! But how could you do that? How could you predict the total after just hearing the first number? Just follow the instructions below!
Instructions/Answer
Here is the trick:
(1) Take the first number and subtract 2 from it then put the number “2” in front of it. (For example, if the number was 67,812, it would be 267,810). That will be the final answer.
(2) Then, when you see the second number your friend writes down you mentally subtract each digit of that number from 9, and write that answer for the third number. (For example, if your friend’s second number is 11,111, then the number you would choose and write down would be 88,888. Or, if your friend’s number is 56,123, then your next number would be 43,876. The key here is that each of your friend’s number digits, when added to the corresponding digit of your number, must total 9.) Then you ask your friend to write down a fourth number, and again you subtract each digit of that number from 9 (do this silently!), and write that answer down as the fifth number. For example, if the second number is 12,345, then you would write 87,654 as the third number because(12345 + 87654=99999). When the 5 numbers, the two of you selected, are all added together, the total will be identical to the number you originally wrote down and set aside! It works every time. Try it and see!
18. Become A Maths Wizard
Now our second trick is a simple, mind-reading party trick. However remember!! it requires a careful performance.
Materials required:
Cut 5 cardboard circles and write seven numbers in every card, as shown in the illustration.
Magic: Place all the cards on the table and declare you will be reading the mind of a member in the audience. Let someone come forward. Ask confidently to think of a number between 1 and 14, and then pick up every card that bears his number. The moment he completes this, you can easily announce his number.
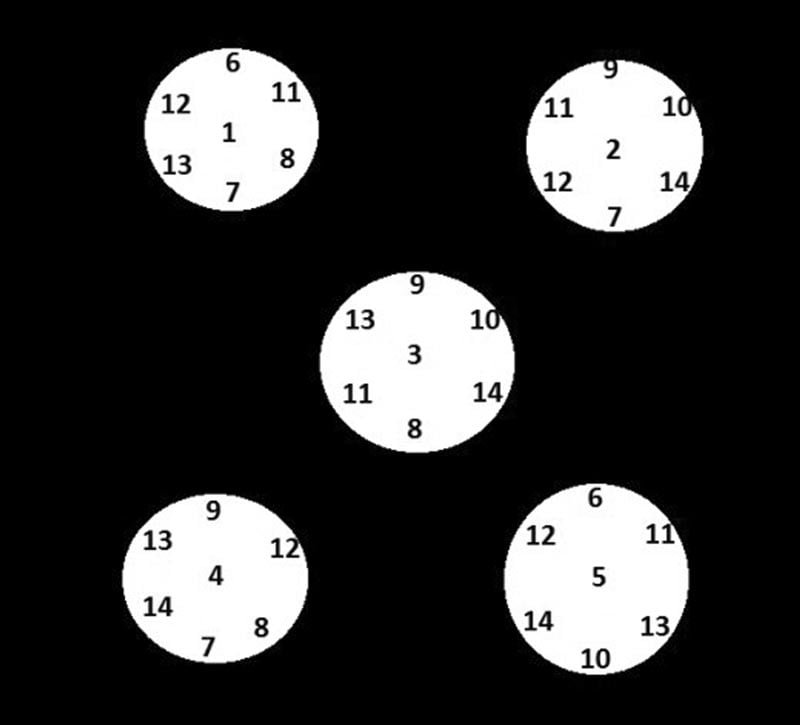
Secret : All you have to do is add the numbers in the middle of every card left over on the table and subtract the sum from 15 to get the number of your choice.
Isn’t it simple?
